Research Lines

Molecular Electronics

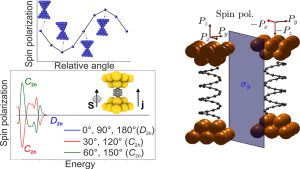
In the foreseeable future, the functionality of electronic devices will rely on the quantum conduction of nanoscopic regions composed of a number of atoms that can range between several thousands down to a single one. The ultimate limit in this miniaturization process is represented by metallic nanocontacts or atomic contacts. In this regard, the most promising research field within nanoscale electronics is probably what is known as molecular electronics. The main goal of molecular electronics is to fabricate functional units for electronic circuits out of very stable and well-characterized molecules such as porphyrins, phtalocyanines, fullerenes, PAH’s (polycyclic aromatic hydrocarbons) or even molecules as large as carbon nanotubes. Graphene deserves attention on its own.

Some representative publications:

Optoelectronics

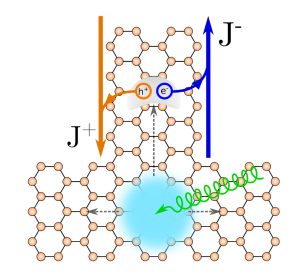The creation of free electron and hole pairs may suffice to broadly explain the optical conductivity of insulators and semiconductors, but, in general, bound electron-hole pairs or excitons also play a non-negligible role. This is particularly true in two-dimensional (2D) crystals, where the excitons become tightly bound due to their confinement and low screening. These include, for instance, hexagonal boron nitride or transition metal dichalcogenides, which have been extensively studied in this regard. Additionally, it has also been shown that non-linear phenomena such as high-harmonic generation and bulk photovoltaic effects can be greatly enhanced in 2D crystals. Furthermore, the high tunability of the atomic structure through strain and the ability to select excitations based on the light polarization render 2D optoelectronics as a very active field from both fundamental and technological perspectives.

Some representative publications:

Two-Dimensional Materials

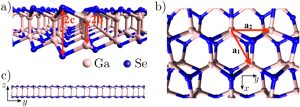Graphene is an allotrope of carbon, whose structure is one-atom-thick planar sheets of sp2-bonded carbon atoms that are densely packed in a honeycomb crystal lattice. The term graphene was coined as a combination of graphite and the suffix -ene by Hanns-Peter Boehm, who described single-layer carbon foils in 1962. Graphene is most easily visualized as an atomic-scale chicken wire made of carbon atoms and their bonds. The crystalline form of graphite consists of many graphene sheets stacked together. Since its discovery, many other two-dimensional materials have appeared, including, to name a few, transition metal dichalcogenides, phosphorene, antimonene, magnetic CrI3, etc.

Some representative publications:

Topological Insulators

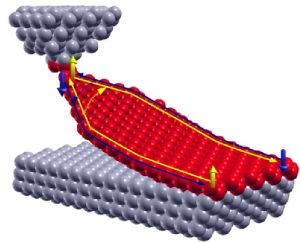 A topological insulator is a material that behaves as an insulator in its interior or bulk while permitting the movement of charges (metallic) on its surface. In the bulk of a topological insulator the electronic band structure resembles an ordinary band insulator, with the Fermi level falling between the conduction and valence bands. On the surface of a topological insulator there are special states that fall within the bulk energy gap and allow surface metallic conduction. Carriers in these surface states have their spin locked at a right-angle to their momentum (spin-momentum locking or topological order). At a given energy the only other available electronic states have opposite spin, so the “U”-turn scattering is strongly suppressed and conduction on the surface is highly metallic. These states are characterized by an index (known as Z2 topological invariants) similar to the genus in topology, and are an example of topologically ordered states.

Some representative publications: 

Quantum Hall Efffect

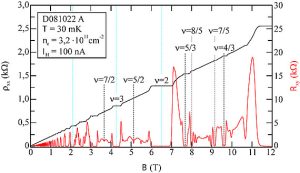The discovery of the quantum Hall effect (QHE) is a remarkable achievement in condensed matter physics awarded with two Nobel prizes. At low temperatures and in strong magnetic fields, it is found that the Hall resistance of a two dimensional electron system has plateaus as a function of the number of electrons. In the integer quantum Hall effect (IQHE), the Hall resistance at the plateaus turns out to be R=h/ne², where n is an integer. In the fractional quantum Hall effect (FQHE), n can be a fractional number. Apart from the fundamental interest of these highly correlated systems, due to the high precision of the measurement, the quantization of the Hall resistance is now used as the standard of resistance.

Some representative publications:

Quantum Dots

Electronic device miniaturization in semiconductors has reached the ultimate limit where the number of electrons present in the device can be tuned at will down to a single electron. These systems have been given the name of quantum dots or artificial atoms since their generic properties are determined by their few-electron configurations much the same as in real atoms. In the figure you can see the top view of a heterostructure where a voltage applied to the metal gates can confine the electrons in the two-dimensional electron gas underneath at will.

Some representative publications:

Vortex Matter

Vortex matter refers to the state of matter where the magnetic field penetrates a superconducting condensate creating vortices.  When the dimensions of the superconducting condensate are comparable to the coherence length only few vortices can coexist in the system. As shown in the figure and in contrast to the usual triangular arrangement in bulk, complex and unique vortex structures are expected to occur due to the competition between geometric confinement and vortex-vortex interaction. Many interesting analogies can be drawn between artificial atoms, type-II superconducting mesoscopic disks in perpendicular magnetic fields, or rotating Bose-Einstein condensates where the role of the electron is played in the latter cases, not by the Cooper pairs or the bosons, but by the vortices.

Some representative publications:

  • Long-range vortex transfer in superconducting nanowires, R Córdoba, P Orús, ŽL Jelić, J Sesé, MR Ibarra, I Guillamón, S Vieira, … Scientific reports 9 (1), 12386 (2019).
Print Friendly, PDF & Email